1. Folding the diagonal of a rectangle

There are many pleasures in origami. For example, when you find that apparently unrelated lines or points meet in a special way, have you asked yourself “Is that really so? Why? How does that work?” If so, then read on.

I’ll show you that certain folding procedures do work and why. The amount of formal mathematics will be minimised to make this as accessible for as many people as possible.

Here’s a simple example from the folding sequence of Starfish. Folding the diagonal in rectangle can be awkward, especially if it’s long and skinny. However, folding two opposite corners together provides two landmarks, and, as if by magic, if you bring these together, a second fold goes exactly through both of the corners.

Now your reaction might be one of these:

1. Great, I’ll use that the next time I have an awkward diagonal to fold. I don’t care why it works – it just seems to. (Instrumental)

2. Hmm, it seems to work, but does it always work, whatever the rectangle’s proportion? I’ll try it on different rectangles and see. (Empirical)

3. Yes, but why does it work? (Desire for a proof)

4. Can I get more out of this by generalising or applying this to other kinds of shapes? (Mathematical)

5. So what? I have no problems folding diagonals! (Irrelevance)

6. It’s obvious that it works. Why do you need a proof? (Triviality)

Let’s concentrate on reaction number 3, looking for a proof , and consider different kinds of proofs:

1. “Traditional” proofs given in schools and textbooks.

2. Proof by looking

3. An illuminating proof that gives insight

4. Proofs that give a feeling of simplicity and inevitability: it must be so.

Traditional proofs proceed logically through a set of steps to “prove that which was to be proved”: QED. However, these proofs can be unsatisfying for several reasons.

1. Some proofs assume something is true and then show that it is. This begs the question: how did you get to know that something is true in the first place?

2. You are expected to start from the beginning and check each logical step. However, some proofs are long, are missing steps, are verbosely longwinded or have tricky steps so that by the end you’ve forgotten where you came from.

3. Some proofs assume vital knowledge that you don’t have.

4. Some “proofs” are demonstrations, not proofs. For example, here is a demonstration that the “sum of the angles in a triangle is 180 degrees”. Some teachers in schools rip the corners, put them together and show that they “seem” to lie on a straight edge. Demonstrations are valuable because they can persuade, but they usually lack sufficient rigour to be convincing.

5. Even if you understand every step, some proofs don’t give you any insight. A classic example is to set up equations and solve them using algebraic techniques. Out pops the answer, but you don’t understand why the answer has to be answer you have, and not something else.

So can we find something better than a traditional proof for our first fold? Along the way we’ll use some tactics that will be useful for solving other problems.

First, we’ll add some more lines to help us. We don’t want these extra lines when folding, but for solving problems they can help us see relationships and make connections.

Second, we’ll try to avoid “special” rectangles so that our observation will be true for all rectangles. The rectangles to avoid have special properties that not all other rectangles share e.g. squares, , , 1:2, etc.

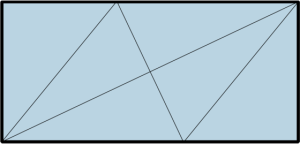
Can you now see why this has to work? We’ll look at this more closely in the next part.